Primícias sobre suportabilidade dos barramentos a esforços mecânicos provenientes de correntes de curto-circuito

Um barramento de 50 kA realmente suporta um curto-circuito de 50 kA? Para um bom funcionamento de todo o sistema, e para evitar surpresas desagradáveis, saber a suportabilidade dos barramentos a serem utilizados em uma instalação elétrica é fundamental. A escolha desse barramento deve ser feita levando em consideração suas condições nominais de operação e também possíveis eventos que podem ser danosos ao mesmo, como por exemplo um curto-circuito.

Neste artigo trataremos de forma detalhada as medidas a serem adotadas a fim de garantir que um barramento tenha plenas condições de suportar os efeitos de uma corrente elevada como a de curto-circuito.

1. CORRENTES ELÉTRICAS E ESFORÇOS MECÂNICOS

A circulação de corrente elétrica através de condutores induz forças eletromagnéticas nos mesmos. Em caso de múltiplos condutores há uma interação entre essas forças eletromagnéticas, causando assim o que chamamos de esforços mecânicos ou tensões mecânicas.

Há uma relação de proporcionalidade entre as tensões mecânicas e as correntes que circulam nos condutores. Diante disso observa-se que o caso de maior atenção é durante um curto-circuito, ou seja, quando há um aumento substancial da corrente elétrica. Posto isto, devemos utilizar, então, em nossos cálculos o valor de pico da corrente de curto-circuito.

2. COMO CALCULAR A SUPORTABILIDADE DE UM BARRAMENTO A UMA TENSÃO MECÂNICA PROVENIENTE DE UMA CORRENTE ELÉTRICA

A determinação da suportabilidade é feita através de diversos cálculos que serão apresentados neste capítulo. A fim de facilitar a sua compreensão o cálculo será dividido em diversos passos devidamente explicados.

É de suma importância lembrar que os passos abaixo servirão para você verificar se um barramento JÁ ESCOLHIDO* tem condições de suportar um curto-circuito sem apresentar rupturas ou deformações. Também é importante que já tenham sido definidas as condições de instalação do mesmo (local de instalação, posição e ventilação).

*O barramento deve ser escolhido previamente da forma tradicional, ou seja, de acordo com suas características nominais de operação.

 

2.1 Cálculo dos esforços mecânicos

Devemos inicialmente calcular os esforços mecânicos gerados pela interação das forças eletrodinâmicas e posteriormente calcularemos os demais pontos de interesse.

A – Força gerada por dois barramentos paralelos

As forças eletrodinâmicas são calculadas pela seguinte equação:

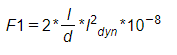
Onde:

• F1: Força expressa em daN;
• I_dyn: Valor de pico da corrente de curto-circuito em A – Calculada conforme a expressão abaixo:

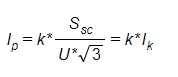
Onde:

• S_sc: Potência de Curto-Circuito;
• I_k: Corrente suportada por um curto período de tempo;
• U: Tensão de operação;
• l: Distância entre os isoladores da mesma fase;
• d: Distância de uma fase a outra;
• k: Para 50 Hz: 2,5 ; para 60 Hz: 2,6 (Segundo IEC) ou 2,7 (Segundo Ansi).

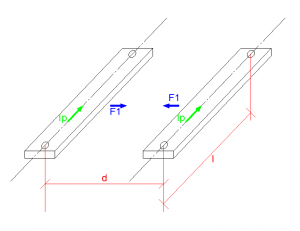
Imagem 1: Forças atuantes e dimensões do barramento

B – Força nos apoios dos barramentos

A força atuante nos apoios do barramento é proporcional a força gerada a partir da interação entre as forças eletromagnéticas nos barramentos e pode ser calculada pela equação abaixo:

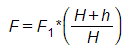Onde:

• F: Força nos apoios;
• H: Tamanho do isolador (ver imagem a seguir);
• h: Distância entre o topo do isolador e o centro de gravidade do barramento.

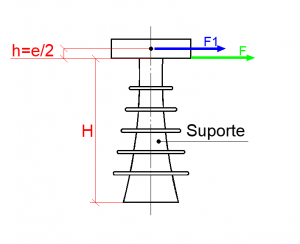
Imagem 2: Detalhe distância isolador

Havendo múltiplos apoios para o barramento determinamos a força em cada um deles com o auxílio da tabela a seguir:

Tabela 1: Valores de kn de acordo com o número de apoios no barramento

A força nos n apoios será proporcional a força F1 calculada anteriormente.  A constante de proporcionalidade é kn, apresentado na tabela acima.

A equação utilizada para o cálculo da força é apresentada abaixo:

Essa força F calculada deve ser menor que a resistência a flexão do suporte (esse dado é obtido diretamente com o fabricante do barramento).

 

C – Esforço mecânico no barramento

Assumindo que o barramento é isolado nos apoios, calcula-se o momento fletor atuante na barra através da equação abaixo:

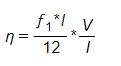
Onde:

• η: Tensão resultante – Deve ser menor que os valores admissíveis para cada tipo de material:

          Cobre 1/4 duro: 1200 daN/ cm²;

          Cobre 1/2 duro: 2300 daN/ cm²;

          Cobre 4/4 duro: 3000 daN/ cm²;

          Alu-Estanhado: 1200 daN/ cm².

 

• F₁: Força entre condutores;
• h: Distância entre o topo do isolador e o centro de gravidade do barramento.
• l: Distância entre os isoladores de uma mesma fase;
• I/V: é o módulo de inércia entre um conjunto de barras ou uma barra;

As expressões usadas para calcular I e I/V variam de acordo com a quantidades de barramentos por fase. Abaixo são apresentadas as equações utilizadas neste estudo:

C.1 Caso com uma barra por fase

 

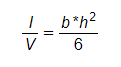
C.2 Caso com duas barras por fase

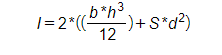
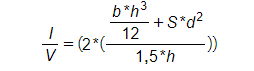
Utilizou-se, também, como referência para os valores de I e I/V a tabela abaixo:

 

2.2 Cálculo da capacidade de condução de corrente do barramento diante de suas condições de instalação

Neste passo calculamos a capacidade máxima de condução de corrente do barramento escolhido diante de suas condições de instalação e de temperatura.

É de suma importância que a corrente aqui calculada seja igual ou superior a corrente nominal definida para o barramento. Caso o resultado seja menor que a corrente esperada deve-se alterar as condições de instalação ou até o mesmo as medidas do barramento a fim de obter o resultado projetado.

Para essa análise utilizamos, também, a tabela 3 da norma IEC 60694 – Especificações comuns para normas de equipamentos de manobra de alta-tensão e mecanismos de comando. Nesta tabela podemos identificar qual a tolerância para o aumento de temperatura no barramento de acordo com material e a isolação do mesmo.

A corrente é calculada pela seguinte equação:

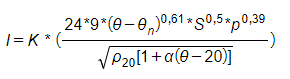
Onde:

• I: Corrente permitida expressa em amperes (A);
• θn: Temperatura ambiente (θn ≤ 40 ºC);
• (θ – θn): Aumento de temperatura permitido de acordo com a Tabela V da IEC 60694;
• S: Seção transversal do barramento (cm²);
• p: Perímetro externo do barramento (cm);
• ρ20: Resistividade do condutor a 20 ºC

Cobre: 1,83 µΩ cm;

Alumínio: 2,90 µΩ cm;

• α: Coeficiente de resistividade da temperatura: 0,004;
• K: Coeficientes relacionados as condições de instalação

1. k1– Fator dado pelo número de barramentos por fase:

• 1 barra: k1=1;
• 2 ou 3 barras, ver tabela abaixo:

Tabela 2: Valores de k1 de acordo com o número de barras

 

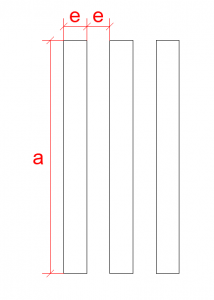
Imagem 4: Dimensões do barramento – MT Partenaire – Schneider Electric

1. k2– Fator relacionado ao tipo de superfície dos barramentos

• Se nu: k2=1;
• Se pintado: k2=1,15.

 

2. k3– Fator relacionado a posição dos barramentos

• Montagem vertical na lateral: k3=1;
• Montagem horizontal na base (1 barra): k3=0,95;
• Montagem horizonta na base (várias barras): k3=0,75.

 

3. k4– Fator relacionado ao local onde os barramentos serão instalados

• Atmosfera interior calma: k4=1;
• Atmosfera exterior calma: k4=1,2;
• Em duto não ventilado: k4=0,80.

 

4. k5– Fator relacionado a ventilação artificial

• Sem ventilação artificial: k5=1;
• Havendo ventilação artificial deve-se tratar caso a caso e com validação através de testes.

 

5. k6– Fator relacionado ao tipo da corrente

• Para corrente alternada de frequência ≤ 60 Hz: k6 é uma função do número n de barras por fase e do espaçamento entre elas.

A tabela abaixo apresenta o valor de k6 para um espaçamento igual a espessura das barras:

Tabela 3: Valores de k6 de acordo com o número de barras por fase com espaçamento entre elas igual a espessura das barras

 

Fez-se o produto de todos os fatores k a fim de encontrar o fator K a ser aplicado na fórmula da corrente apresentada anteriormente.

Diante de todos esses fatores calculamos a corrente com a equação apresentada anteriormente. Caso a corrente calculada seja maior ou igual a corrente máxima do barramento escolhido devemos seguir para o próximo passo. Caso a corrente calculada seja menor deve-se reavaliar as condições de instalação do barramento, ou até mesmo as dimensões do mesmo.

 

2.3 Cálculo do aumento de temperatura gerado por um curto-circuito

Após garantir que o barramento é capaz de atender plenamente as condições projetadas diante das condições de instalação, agora faz-se o cálculo do aumento de temperatura após um curto.

A variação de temperatura é encontrada pela seguinte equação:

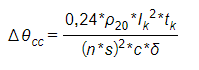
Onde:

• Δθ_cc: Aumento da temperatura após um curto-circuito;
• c: Calor específico do metal:

Cobre: 0,091 kcal/kgºC;

Alumínio: 0,23 kcal/kgºC;

• S: Seção transversal de um barramento (cm²);
• n: Número de barramentos por fase;
• I_k: Corrente suportada por um curto período (1 a 3 segundos);
• t_k: Tempo de duração (1 a 3 segundos);
• ρ₂₀: Resistividade do condutor a 20 ºC:

          Cobre: 1,83 µΩ cm

          Alumínio: 2,90 µΩ cm

• δ: Densidade do metal:

         Cobre: 8,9 g/cm³;

         Alumínio: 2,7 g/cm³;

• (θ – θ_n): Aumento de temperatura permitido.

Sabendo a variação da temperatura durante o curto calculamos então a temperatura no condutor após o evento da seguinte maneira:

Onde:

• θ_n: Temperatura ambiente;

θ_t  deve ser menor ou igual ao valor admissível previsto na tabela 3 da norma IEC 60694. Estando dentro do parâmetro definido pela norma podemos ir para o próximo passo.

 

2.4 Frequência de Ressonância

Por fim é calculada a frequência de ressonância a fim de verificar se o barramento escolhido não se encontra em uma faixa de frequência que ofereça perigo ao seu bom funcionamento.

Consideramos em nosso estudo dois intervalos de frequências que devem ser evitados, sendo eles:

1. 60 Hz ±16% – Portanto, frequências entre 50 e 70 Hz devem ser evitadas.
2. 120 Hz ±16% – Portanto, frequências entre 100 e 140 Hz devem ser evitadas.

A frequência de ressonância do barramento é dada pela equação abaixo:

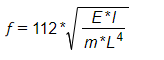
Onde:

• f: Frequência de ressonância (Hz).
• E: Modulo de elasticidade do material:

          Cobre = 1,3 x 10⁶ daN/ cm²

          Alumínio = 0,5 x 10⁶ daN/ cm²

• m: Densidade linear do material ( ver tabela apresentada na imagem 3).
• L: Distância entre os suportes.
• I: Momento de inercia do barramento ( ver tabela apresentada na imagem 3).

3 – CONCLUSÕES

É de suma importância que os barramentos estejam dentro dos limites aceitáveis em todos os aspectos listados no capítulo anterior. Havendo valores inesperados deve-se reanalisar o sistema proposto a fim de evitar problemas futuros.

 

Fonte: Engenheiros Associados

Leia mais artigos como este clicando aqui